Introduction to Regression: Understanding the Basics

Benjamin Chen
2022年1月17日
讀畢需時 4 分鐘

已更新：2024年1月19日

Hello! Welcome to this series on Regression Analysis. Throughout this series, we will uncover key topics in the field of regression. To give you an idea of what we will go through, here is an overview of our agenda:

1. Simple Linear Regression

2. Multiple Regression – General

3. Multiple Regression – Multicollinearity

4. Multiple Regression – Comparing Two Regression Models

5. Multiple Regression – Variables Selection Strategies

6. Multiple Regression – Dummy Variables and Interaction Terms

7. Multiple Regression – Transformation Terms

8. Logistic Regression

I will try to break down each topic into simple terms but keep in mind this will not be an easy area to study. So, let's take this step by step. In this story, I will introduce regression and the foundations that are required.

What is Regression?

In simple terms, regression studies the relationship between response variables (also called outcome/target/dependent variables in other contexts) and predictor variables (also called explanatory/features/independent variables in other contexts).

To illustrate what I mean, consider the following scatterplot:

We have sleep time on the x-axis and grumpiness on the y-axis. We can observe that when someone sleeps less, they are grumpier. This is a very simple example of regression. We are trying to explain the relationship between sleep time and grumpiness. Typically, the y-variable is our response variable, and the x-variable is our predictor variable. So, in a sense, we want to use sleep time to explain or predict grumpiness.

Types of Variables

The type of variable will usually affect how we want to perform regression analysis, so it’s important to understand them first. Let’s go through them one by one.

There are two main types of variables, categorical (qualitative) and numerical (quantitative).

Categorical/Qualitative

If your variable value is in discrete groups or ‘categories’, then you have a categorical variable. An example would be Gender, where it takes on values in ‘categories’ like “Male” and “Female”.

If we want to be a little more specific, then we have nominal and ordinal variables.

Nominal

A nominal variable is a type of categorical variable with no specific order or scale. Take Color as an example. Color can take on values like “Blue”, “Red”, “Green” and “Yellow”. There are no specific orders between these values. When a nominal variable takes on only two values, we refer to it as a binary variable. An example of a binary variable is Gender that only has 'Male' and 'Female' as its value.

Ordinal

On the other hand, an ordinal variable is a type of categorical variable with an order. An example of an ordinal variable could be socio-economic status. If socio-economic status takes on values like “low income”, “medium income” and “high income”, you can see that there is an order between the different categories.

Numerical/Quantitative

If your variable value is a number, then you have a numerical variable. An example would be the Number of Students, which takes on the values of numbers. We have two types of numerical variables, discrete and continuous.

Discrete Numerical Variable

Discrete numerical variables are variables that can be counted. In other words, discrete numerical variables can only take on integer values. An example would be the Number of Students. The number of students can only be an integer. It doesn’t make sense to have a fraction of a student (eg. 10.3 students)

Continuous Numerical Variable

Continuous numerical variables are variables that can be measured. They can be any value within a specific range. So, any variables that take on decimals or fractions are continuous numerical variables. For example, height is a continuous numerical variable. It can take on fractional values like 17.43 centimeters or 1.98 meters.

Important Descriptive Statistics

In case you have forgotten the basics of statistics, let’s also recap two important descriptive statistics, the mean and standard deviation.

Mean

The mean is the average value. It can refer to either the population mean or the sample mean, denoted by mu (greek letter) and X bar, respectively. We can find the mean by summing up all the values and dividing them by the number of values. Their formulas are as follow:

Population Mean:

Sample Mean:

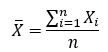
Capitalized N stands for the population size and lowercase n stands for the sample size. These notations are important, so please remember the difference.

Standard Deviation

Next, we have the standard deviation, which measures the spread of a distribution. Likewise, it can refer to the population standard deviation or the sample standard deviation. The greater the standard deviation, the greater the spread. We can find the standard deviation by taking the square root of the variance.

Population Standard Deviation:

Sample Standard Deviation:

Notice that the sample standard deviation actually divided by n-1 instead of n. If you’re curious why this is the case, you may refer to the following answer in the box.


To put it simply, (n−1) is a smaller number than (n). When you divide by a smaller number you get a larger number. Therefore, when you divide by (n−1), the sample variance will work out to be a larger number. 

Let's think about what a larger vs. smaller sample variance means. If the sample variance is larger, then there is a greater chance that it captures the true population variance. That is why when you divide by (n−1) we call that an unbiased sample estimate, whereas dividing by (n) is called a biased sample estimate. 

Because we are trying to reveal information about a population by calculating the variance from a sample set we probably do not want to underestimate the variance. Basically, by just dividing by (n), we are underestimating the true population variance, that is why it is called a biased estimate.

Ok, that might be slightly confusing. If you're unsure of this explanation and want to understand, you may need to go back and review inferential statistics. But this is no big deal for regression. You'll do just as fine by memorizing the formula.